Mathematics of parking tickets

I confess I sometimes don’t pay the parking meter when I just need to pop into a store to quickly grab an item. In times like these, the risk of a ticket can feel … worth it — but is it?

To decide, we posit that parking enforcement officers random walk about and effectively check a given spot with rate \(\lambda\) (E.g., if they stop by each spot on average once every two hours, then \(\lambda = 1 / 2\), here). We suppose the cost of the ticket is \(C\). If we leave our car at a meter for time \(t\) without paying for parking, the expected cost in tickets is then (a result from Poisson stats)

\begin{eqnarray} \label{gen} \tag{1} E(\text{cost}(t)) = C \left [ 1 - \exp(-\lambda t) \right]. \end{eqnarray}

For small times, it’s interesting to consider the cost per minute. To that end, we write \(t = m / 60\) and expand the above. This gives

\begin{eqnarray}\tag{2} \label{expand} E(\text{cost}(m)) = C \left [ \frac{m \lambda }{60} - \frac{1}{2} \left( \frac{m \lambda }{60}\right)^2 + \ldots \right] \end{eqnarray}

The expected cost per minute then is

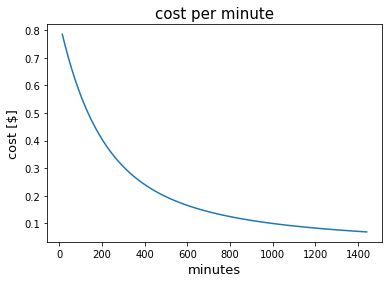
\begin{eqnarray}\tag{3} \label{cost_per_min} \frac{E(\text{cost}(m))}{m} = C \left [ \frac{\lambda }{60} - \frac{m}{2} \left( \frac{\lambda }{60}\right)^2 + \ldots\right] \end{eqnarray}

Notice that this is a decreasing function of \(m\) — the longer we leave the spot alone, the cheaper it gets per minute to risk a ticket. This occurs because we are guaraneed a ticket at long times, so the cost per minute at long times must approach \(C / m\), a decreasing function of \(m\) (this assumes we can’t get more than one ticket per day — perhaps wrong?).

Data: Suppose \(C = 100\) and \(\lambda = 1 / 2\). Then the expected cost per minute to not pay the meter is roughly \(\frac{100}{2 * 60} = 0.83\). Very sobering: In general, it costs much less to simply pay the meter. Alas, I am a weak man. I worry in future I’ll continue to think it’s worth a mere \(83\) cents a minute of risk while I rush in to grab that needed part from my local Ace Hardware. And if it takes a little longer, … meh, the price per minute goes down over time.

import numpy as np
%pylab inline

c = 100
Lambda = 1 / 2.
t_values = np.linspace(0, 24, 100)

fig, ax = plt.subplots(1,1, figsize=(6,4))
ax.plot(
    t_values * 60.,
    c * (1 - np.exp(-t_values * Lambda)) / (60 * t_values),
)
ax.set_title('cost per minute', fontsize=15)
ax.set_xlabel('minutes', fontsize=13)
ax.set_ylabel('cost [$]', fontsize=13)

Jonathan Landy Jonathan grew up in the midwest and then went to school at Caltech and UCLA. Following this, he did two postdocs, one at UCSB and one at UC Berkeley. His academic research focused primarily on applications of statistical mechanics, but his professional passion has always been in the mastering, development, and practical application of slick math methods/tools. He currently works as a data-scientist at Stitch Fix.

Mathematics of parking tickets

Published

Category

Contact